Application of the microcanonical ensemble: two-state system

Additional Readings for the Enthusiast

McQuarrie [3], Chapter 1, Chapter 2.1

Chandler [1], Chapter 3.1-3.4

Goals for today’s lecture

• Derive a physical observable in the context of the microcanonical ensemble.

• Understand and apply Stirling’s approximation from last lecture.

Problem Statement

In the last lecture, we introduced the concept of the microcanonical ensemble, which we defined as the set of all possible microstates associated with a macrostate in which the number of particles (\(N\)), the volume (\(V\)), and the energy (\(E\)) are constant. We then defined several postulates of statistical mechanics, which we summarize as:

• \(Y_\textrm{obs} = \langle Y \rangle\): the ergodic hypothesis, where \(\langle Y \rangle = \sum_i^\textrm{states} p_i Y_i\)

• \(p_i = \frac{1}{\Omega(N,V,E)}\): the principle of equal a priori probabilities, where \(\Omega(N,V,E)\) is the degeneracy (or number of states) of the microcanonical ensemble

• \(S = k_B \ln \Omega(N,V,E)\): the definition of the Boltzmann entropy.

We will now use an example to illustrate how the microcanonical ensemble can provide information about the thermodynamic properties of a system.

Consider a polymer chain that adsorbs to an attractive surface.

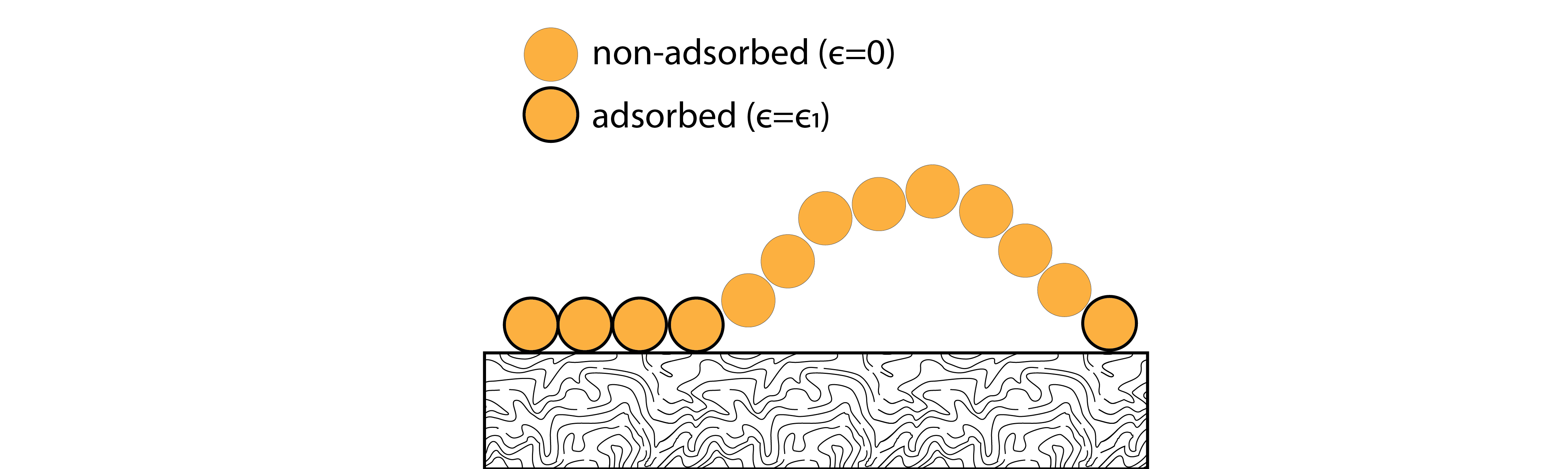
The chain is composed of \(N\) monomers that do not interact with each other. The surface is attractive such that a single monomer adsorbs favorably with an energy \(-\epsilon\). If we assume the energy of the free monomers is 0 and there are no monomer-monomer interactions, then the total energy of the system for \(n\) adsorbed monomers is:

\[E = \sum_i^N \epsilon_i = -n \epsilon\]

The question we will ask is - how does the energy of the system (or, equivalently, the number of adsorbed monomers) depend on the temperature?

To start – what relationships do we know for our system?

• \(E = -n \epsilon\) from the microscopic description of the system given above

• \(S = k_B \ln \Omega (E)\) from the definition of the entropy of the microcanonical ensemble using the shorthand version of \(\Omega(N,V,E)\)

• \(T = \left ( \frac{\partial E}{\partial S} \right )_V\) from thermodynamics

Given these relationships, we can use the equations of the microcanonical ensemble to relate the degeneracy to the entropy and then identify a relationship between the energy and temperature from thermodynamics. Thus, we will describe our system as having a constant energy - that is, we assume that \(n\) and \(E\) are fixed and then will derive a temperature dependence based on this assumption. There may be another ensemble that is more appropriate - for example, we may assume the temperature is constant, instead, and choose a different ensemble (e.g. the canonical ensemble) to solve for the temperature dependence. If we are consistent in our assumptions and mathematical framework, then any ensemble is fine (as long as the fixed thermodynamic variables in the ensemble do not violate some feature of the system) and we will return to this problem with alternative ensembles in future lectures.

We need to start by computing an expression for the degeneracy. Recalling previous sections, we know that \(\Omega(E)\) is defined as the number of microstates that have the same energy \(E = - n\epsilon\). Since the number of total monomers, \(N\), is greater than the number of adsorbed monomers, \(n\), there are many possible ways to choose the the set of \(n\) adsorbed monomers from the total set of \(N\) monomers, but any set of \(n\) that we select will have the same energy. Therefore, the degeneracy of this system is equal to the number of unique ways to select \(n\) monomers that adsorb to the surface out of the possible set of \(N\) - or in other words, the number of unique ways to split the \(N\) monomers into two groups (adsorbed and free). Computing this quantity will motivate a mathematical aside.

Relevant Mathematics

Combinatorics

Imagine that you have \(N\) objects. In general, objects can either be

distinguishable

objects that can be told apart, such as playing cards, or

indistinguishable

objects that cannot be told apart, such as marbles

A common question we will face is how many ways we can uniquely divide \(N\) distinguishable objects into groups. We can calculate this using playing cards as an example. First, we can count the number of unique ways to shuffle a deck of \(N\) distinguishable playing cards. We can imagine placing the first card on the top of the deck; there are \(N\) possible choices for the first card. Next, we can imagine placing the next card on the top of the deck. Since we have removed 1 card, there are now \(N-1\) choices remaining, so there are \(N(N-1)\) unique choices for placing the first two cards, and so on. This leads to:

\[\begin{split}\begin{aligned} \text{# of arrangements} &= N(N-1)(N-2) \dots (2)(1) \nonumber \\ &= N! \end{aligned}\end{split}\]

If the playing cards were instead indistinguishable, then there would instead be only unique 1 arrangement of playing cards (since switching the order of any two cards would make the order look exactly the same). Now, we consider the question how many ways there are to divide \(N\) distinguishable playing cards into two groups, one containing \(n_1\) cards and the second containing \(N-n_1\) cards. Following the same reasoning as above, for the first group we have \(N\) options for the first card, \(N-1\) for the second, and so on, until for the last selection we have \(N-n_1+1\) choices. The total number of arrangements for group 1 is thus:

\[\begin{split}\begin{aligned} N(N-1)(N-2)\dots(N-n_1+1) &= \frac{N(N-1)(N-2)\dots(2)(1)}{(N-n_1)(N-n_1-1)\dots(2)(1)} \nonumber \\ &= \frac{N!}{(N-n_1)!} \end{aligned}\end{split}\]

The second group has \(N-n_1!\) choices for placing the remaining \(N-n_1\) cards, so that in total there are \(\left [ N!/(N-n_1)!\right ] \times (N-n_1)! = N!\) arrangements of the two groups.

However, the question asked for how many ways there are to divide them into two groups; the arrangement of cards within each group does not matter, as placing the same \(n_1\) cards in the group in any order is still the same division. There are \(n_1!\) ways to arrange the \(n_1\) cards in the first group and \((N-n_1)!\) ways to arrange the cards in the second group, so in total we have overcounted by \(n_1!(N-n_1)!\) since every division into a group of \(n_1\) and \(N-N_1\) was counted an extra \(n_1!(N-n_1)!\) times associated with different orders of the cards. Thus, the total number of unique ways of dividing the cards into two groups if the order within each group doesn’t matter is:

\[\text{# of divisions} = \frac{N!}{n_1!(N-n_1)!}\]

This expression appears in the binomial expansion and is referred to as the binomial coefficient, and can be expanded to any number of groups following similar reasoning.

Stirling’s approximation

We have just seen an example of a calculation that uses factorials, which can become difficult to treat algebraically. Fortunately, there is an approximation that simplifies the use of factorials. Because \(N!\) is a product, it is easier to deal with \(\ln N!\) which is a sum. We can write:

\[\ln N! = \sum_{m=1}^N \ln m\]

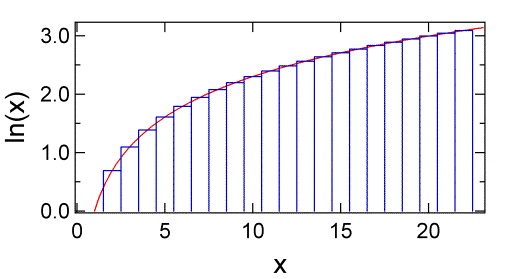
The value of this sum is equal to the total area of a series of rectangles, each with height \(\ln m\) and width \(dm = 1\). That is, we can equate the sum to the integral of \(\ln m\) using rectangular integration.

As \(N\) increases, the difference between successive terms in the sum will become very small - if \(N \gg 1\), the difference in the terms becomes:

\[\begin{aligned} \ln (m+1) - \ln m = \ln \frac{m+1}{m} \approx \ln 1 \approx 0 \quad \text{for $m\gg1$} \end{aligned}\]

Therefore, for \(N\gg1\) we can replace the sum over discrete values of \(m\) with an integral over continuous values of \(m\) - effectively allowing the width of each rectangle (\(dm\)) to shrink to an infinitesimal value. The error between the approximation using an integral and the exact sum over integer values of \(m\) is very small once \(N\) is large. The resulting approximation allows us to write:

(14)\[\begin{split}\ln N! &= \sum_{m=1}^N \ln m \nonumber \\ &\approx \int_1^N \ln m dm \quad \text{if $N \gg 1$} \nonumber\\ &= \boxed{N \ln N - N} \end{split}\]

Equation (14) is Stirling’s approximation, and differs by less than 1% from \(\ln N!\) if \(N > 50\). We will make frequent use of Stirling’s approximation, and moreover we will often approximate summations as integrals, throughout the course. We will return to solving the example using Stirling’s approximation and combinatorics in the next lecture.

Back to the example

Reminder, our overarching question is: how does the energy of the system (or, equivalently, the number of adsorbed monomers) depend on the temperature?

Having defined methods for splitting objects into two groups, we can now count how many ways there are to separate \(N\) monomers into a group of \(n\) that are adsorbed to a surface and \(N-n\) that are not which defines the degeneracy of a microcanonical ensemble with \(\langle E \rangle = n\epsilon\).

We thus write an expression for \(\Omega(E)\) and the entropy based on the combinatorics expression above:

\(S = k_B \ln \left ( \frac{N!}{n!(N-n)!} \right )\)

[Show derivation]

\[\begin{split} \Omega(E) &= \frac{N!}{n!(N-n)!}\\ S &= k_B \ln \Omega(E) \\ &= k_B \ln \frac{N!}{n!(N-n)!} \\ \end{split}\]

\(S = -k_B N \left[\alpha \ln \alpha + (1-\alpha)\ln(1-\alpha)\right]\), where \(\alpha \equiv n/N\)

[Show derivation]

First, some algebra,

\[ S = k_B \left[\ln(N!) - \ln(n!) - \ln[(N-n)!]\right] \]

Using Stirling’s approximation,

\[\begin{split} S &= k_B \left[N\ln N - N - n\ln n + n -(N-n)\ln(N-n) + (N-n)\right]\\ &= k_B \left[N\ln N - n\ln n -(N-n)\ln(N-n)\right]\\ \end{split}\]

Replacing all \(n\) with \(N \alpha\)

\[\begin{split} &= k_B \left[N\ln N - N\alpha \ln (N\alpha) -(N-N\alpha)\ln(N-N\alpha)\right]\\ &= k_B N \left[\ln N - \alpha \ln (N\alpha) -(1-\alpha)\ln(N(1-\alpha))\right]\\ &= - k_B N \left[\alpha \ln \alpha + (1-\alpha)\ln(1-\alpha)\right]\\ \end{split}\]

With this equation relating the entropy and our number of adsorbed monomers, and our earlier equation relating the energy to the number of adsorbed monomers, we can determine the temperature dependence of the latter by using

\[ \left ( \frac{\partial E}{\partial S} \right )_V = T \]

Given that the relationship \(\frac{\partial S}{\partial E}\) is more well-defined, we flip our equation:

\[ \left ( \frac{\partial S}{\partial E} \right )_V = \frac{1}{T} \]

\(n = \frac{N}{ 1 + e^{-\epsilon / k_BT}}\)

[Show derivation]

\[\begin{split} \left ( -\frac{\partial S}{\partial (n\epsilon)} \right )_V &= \frac{1}{T} \\ -\frac{1}{\epsilon}\left (\frac{\partial S}{\partial \alpha}\right)_V\left (\frac{\partial \alpha}{\partial n} \right )_V &= \frac{1}{T} \\ \end{split}\]

where

\[\begin{split} \left(\frac{\partial S}{\partial \alpha}\right)_V = k_B N \left[\ln(1-\alpha) - \ln\alpha\right]\\ \left(\frac{\partial \alpha}{\partial n}\right)_V = \frac{1}{N} \end{split}\]

such that

\[\begin{split} \frac{-k_B}{\epsilon}\left[ (\ln(1-\alpha) - \ln\alpha) \right] &= \frac{1}{T} \\ \ln(\frac{1}{\alpha}-1) &= \frac{-\epsilon}{k_B T} \\ \frac{1}{\alpha} &= 1 + e^{-\epsilon / k_BT} \\ \frac{N}{n} &= 1 + e^{-\epsilon / k_BT} \\ \end{split}\]

(15)\[ n = \frac{N}{1 + e^{-\epsilon / k_BT}} \]

Equation (15) relates the number of adsorbed monomers to microscopic features (i.e. the adsorption energy per monomer and total number of monomers) as a function of the system temperature.

As \(T\) goes to 0, we expect the system to be in an energy-minimizing configuration with all monomers bound - indeed, as \(T\rightarrow 0\), \(n\rightarrow N\), indicating that all monomers adsorb.

In the opposite extreme, as \(T \rightarrow \infty\), \(n\rightarrow N/2\), indicating that at infinite temperature exactly half of the monomers bind to the surface. This makes conceptual sense - if we have infinite thermal energy, the energy for adsorption is negligible so adsorbing or not adsorbing is equally likely for each monomer (we will revisit this result in future lectures).

This example illustrates the basic principles of the statistical mechanics approach:

• we begin by identifying a set of constant macroscopic thermodynamic variables for the system (\(NVE\)),

• choose an appropriate statistical ensemble (microcanonical) corresponding to these variables,

• calculate the value for a thermodynamic variable (entropy) from ensemble properties based on our microscopic picture of the system,

• then use thermodynamic relations to get additional information about the system (temperature).

Why does our final result seem to contradict our assumption that energy is constant?

[Click for answer]

Recall that the problem statement itself (i.e. the microscopic description of the system) does not specific a constant energy - we **choose** to describe our system in such a way that the energy is held constant, then apply the equations of the microcanonical ensemble (consistent with our choice) to derive the temperature dependence. We also could have derived the same result by assuming that the system is held at constant temperature and that the energy is allowed to vary, and achieve the same result (we will do this next lecture). We will find several variations of this basic approach, and will illustrate that the correct choice of thermodynamic variables, even for the same system, can dramatically simplify problem solutions.

Link to Shared Notes